This suite of applications aims to develop an intuitive visual understanding of the chronogeometric nature of Minkowski spacetime (a term explained later), i.e., the spacetime of Special Relativity. In explaining what the applications show, I also explain the basics of special-relativistic kinematics. You can download the applications or run them directly in your browser at any time by clicking the hyperlinks on the left side of the page. For a short set of instructions for how to download and run the applications, click on the final section in the navigational menu to the right of the page.
The first two applications, LC.jar and RELSIM.jar, are user-interactive animations based on thought experiments proposed by Hermann Bondi in his book 'Relativity and Common Sense.' The final application comprises a user-interactive pair of Minkowski diagrams. LC.jar makes a visual demonstration that, given that the speed of light is independent of that of its source and thus the same for all observers, a measurement of a moving rod will give a value that is less than, i.e. contracted with respect to, a measurement of that the rod in its own frame of reference. RELSIM.jar, demonstrates in a similar way that, given that the speed of light is the same for all inertial observers (an inertial observer is an observer moving with constant velocity), inertial observers moving with respect to each other will differ in their accounts of which distant events occur simultaneously.
What is it that we mean by "event"? An event, in this context, is some change in the way the world is. For example, the flipping of a light-switch is an event, as is the resulting emission of electromagnetic radiation from the lightbulb connected with the circuit. Surely even these events are composed of other, smaller events. For example, the flipping of a light-switch can be further broken down into several occurrences, including the moment the hand of the person turning the switch makes contact with the switch. But even this "moment" can be further broken down into a series of events in which the hand and the switch become ever closer, until they are close enough for the electrons on the edge of the switch and the electrons on the edge of the hand to be appreciably interacting, and so forth. Thus regard an event as an abstraction from a continuous process, with each of these processes being said to occupy what is called a finite four-volume. This is to say, they occupy a certain region of three-dimensional space, and occur for some finite duration of time. An ''event'' for present purposes is then the comparison of the three-dimensional region of interest before and after some small time interval.
Let us now define "frame of reference", another term I will employ frequently. A frame of reference is a system of identifying places and times of events. If you are an observer watching a rod move with respect to you, you say, as time increases, that the rod occupies different places -- the frame of reference of you, the observer, is the one in which the assignments of places and times of events is such that the moving rod is observed. If "you are the rod", on the other hand, (you can imagine yourself holding a rod if you like), from this perspective, the rod is not changing places as time goes on -- this is the frame of reference in which all events comprising the events of the rod occur at the same place as time goes on.
Here, I offer a way into understanding the kinematics of Special Relativity heavily influenced by that given by Hermann Bondi in his book "Relativity and Common Sense," beginning with the premise that the speed of light is independent of that of its source and thus the same for all observers (the "light postulate" - see Brown and Maia 1993 ) and reflecting on what assignments of locations and times of events could mean depending on one's frame of reference.
Let us think about the consequences of the light postulate for our measurements of the places and times of events. Experience tells us that the quickest way for us as human beings to get information about an event is through light. For example, a lightning strike is always observed visually before the ensuing clap of thunder is heard audibly. Since light, or, more generally, electromagnetic radiation, is our best way of gathering information about events, let us take radar -- sending pulses of electromagnetic radiation and receiving them back -- as our method for determining places and times of events.
To determine consequences of the light postulate for assignments of places and times of events by relativitely moving observers, we need a meaningful concept of relative velocity on the basis of the above mentioned radar technique.
The velocity of an object relative to an observer is, after all, determined by the successive determinations of the places and times of an object. Let us start with something easy to grasp: we know relative motion is possible -- this is a given of experience. Given that relative motion is possible, it follows that if I send out radar pulses at a fixed interval of time, say one second, then somebody moving with respect to me in the direction these radar pulses have been sent will receive them at some fixed interval of time which is larger than the interval of time at which I sent them, simply because they have moved between the sending of each pulse. We will call the ratio of the time interval at which the observer moving with respect to me receives these radar pulses to the time interval at which I send them "k." Thus if I send radar pulses every second, the moving observer will receive them every k seconds, where k > 1. By symmetry, if this moving observer sends out light pulses every one second by their time, I will recieve them every k seconds as well. This serves as the basis for Hermann Bondi's so-called k-calculus for Special Relativity.
How is this ratio k related to my determination of the relative velocity of myself and this relatively moving observer? Let us first take as our units seconds for time and light-seconds for distance (one light second is the distance light covers in a second -- and is ~300,000 km or ~186,000 miles). In these units, the speed of light is c = 1. Say at some time t = 0, the observer whose velocity relative to me I am trying to measure is momentarily at the same location as I am. If I send out a radar pulse, directly at the observer moving with respect to me, at some time \( t = t_{0} \), then this observer will receive the radar pulse at a time \( t_{r}' = k t_{0} \) in their time. Then, if this observer instantaneously sends a radar pulse back, which is equivalent to considering the reflection of the radar pulse I initially sent, it follows that I will receive the radar pulse at \( t = t_{2} = k t_{r}' = k^2 t_{0} \). So I sent out a radar pulse at \( t_{0} \), and received it back at \( t_{2} = k^2 t_{0} \). At what time should I say this event (the reflection of the radar pulse) occurred? Certainly the only reasonable choice is half way between the times of receiving and of sending the pulse, at \( t_{r} = \frac{t_{2}+t_{0}}{2} = \frac{(k^2 + 1)t_{0}}{2} \). How far away should I say this event was? Well, I know the total time it took the pulse to leave and return to me is \( t_{2}-t_{0} \). Since this is the round trip time, I should say it took \( \frac{(t_{2}-t_{0})}{2} \) seconds to reach the moving observer. Thus, I should say that the event was \( \frac{t_{2}-t_{0}}{2} = \frac{(k^2 -1)t_{0}}{2} \) light-seconds away. So, I say that in a time \( t = \frac{(k^2 + 1) t_{0}}{2} \) seconds, the moving observer has traversed a distance of \( d = \frac{(k^2 -1)}{2} \) light-seconds, and thus has a velocity of \( v = \frac{d}{t} = \frac{k^2-1}{k^2 + 1} \) light-seconds / second.
This value is always less than one even as k goes to infinity -- nothing can travel faster than the speed of light according to this most reasonable way of determining distances and times of events, and thus also of relative velocity. If we were to come up with independent systems for measuring temporal intervals and spatial intervals -- meters and seconds, for example, and take c to have conventional units, e.g. \( c = 3 \times 10^8 \) m/s, the radar technique would lead such an observer to ascribe a distance to the radar reflection-event of \( d = \frac{(k^2 -1)t_{0}}{2}c \), and thus the relatively moving observer a velocity of \( v = \frac{k^2-1}{k^2 + 1}c\). We can also understand this result in a more directly intuitive way, although one that is qualitative and less well-defined, without ever introducing the k-calculus: if the speed of light is the same for all observers, then light being sent from an observer moving away from you in the direction this observer is moving away from you is still moving at the speed of light with respect to both you and that observer. Thus, since, in the frame of the observer moving away from you, light still moves at the same speed of light away from them, that observer can never catch up to a light ray.
We can now also derive a curious feature of how my timing of events the observer moving away from me undergoes compares to the timing of the same events according to the relatively moving observer. The observer moving away from me was hit by my radar pulse at a time according to them of \( t_{r}^{'} = k t_{0} \), and I determined the time of this reflection to be \( t_{r} = \frac{(k^2 + 1)t_{0}}{2} \). Thus, the time at which the event happened for me compared to the time the event happened for the moving observer is \( \frac{t_{r}}{t_{r}'} = \frac{k^2 + 1}{2k} \). Of course, this relation was derived for only one event for the moving observer -- the reflection of my radar pulse. But I could have chosen to illuminate my moving friend at any time, and thus this relation should hold for all events comprising the moving observer. Given that this event of radar pulse reflection is not unique, and given our expression \( \frac{v}{c} = \frac{k^2-1}{k^2 + 1} \), we derive a general relation between the spacing of times of events in the relatively moving frame as compared to the times of those same events for me of \( t = \frac{k^2 + 1}{2k} t' \). Defining \( γ := \frac{k^2 + 1}{2k} \), this becomes \( t = γt' \). This is known as time dilation. We can find γ in terms of \( \frac{v}{c} \):
But, you could say, doesn't this present a paradox, by the symmetry of the k-calculus, as this thought experiment could just as well apply to the moving observer sending radar pulses at me, thus leading us to the result \( t' = γt \)? Equivalently, couldn't we simply rename t to t' and t' to t? This is certainly true -- however, all that would be truly paradoxical would be if these thought experiments, applied in the two different ways just discussed, predicted in one case that upon bringing clocks accompanying the two observers back together (clocks are just controlled sequencings of events / processes), clock 1 would be behind clock 2 (1 and 2 simply serving as names to differentiate the clocks, and behind meaning a constant offset, rather than a lagging rate), and in the other case predicted that clock 2 would be behind clock 1. Since the two observers in this thought experiment are moving away from each other, bringing these clocks together would require that one or both of these observers accelerate. Acceleration is subtle to treat in Special Relativity, and is largely beyond the scope of this lesson. (See the final section of this lesson for some details here.) For now, then, simply suppose that the observer moving with respect to me tosses their clock to, or at least synchronizes their clock with that of, an observer moving with the same magnitude of velocity but towards me at some time. Since in the time dilation factor, only the velocity squared matters, it follows that clock of that observer moving towards me will be behind (again only in offset) my clock. This is the essence of the twin paradox, as can be more generally explained after building up a more complete understanding of Minkowski spacetime.
Having developed the k-calculus, I am now ready to explain the user-interactive applications.
This application serves as a visualization of a thought experiment of Hermann Bondi's, on the basis of the k-calculus and using radar to measure distances and times, that goes as follows: consider a rod moving with respect to some observer such that the relative motion is characterized by the above described ratio k. In order to measure the length of this rod, the observer must send out two radar pulses spaced such that they reflect from the two ends of the rod, according to the observer, at the same time. If we say that the rod passed the observer at time t = 0, say the time at which the first radar pulse, that hits the far end of the rod, is sent out \( t = t_{1}\), say that the second radar pulse, that hits the near end of the rod, is sent out \( t = t_{2} \), call the time at which the first pulse is recieved back by the observer who sent it \( t = t_{3} \), and call the time at which the second pulse is recieved back by the observer who sent it \( t = t_{4} \), then, in order for the two ends of the rod to have been measured at the same time by this observer, it must be that
\begin{equation} \frac{1}{2}(t_{1} + t_{4}) = \frac{1}{2}(t_{2} + t_{3}) \end{equation}We also know that, by the definition of k,
\begin{equation} t_{3} = k^2 t_{2} \end{equation}According to this observer, at the time of reflection according to them, the far end of the rod is at a distance, in light-seconds, of \( \frac{1}{2}(t_{4}-t_{1}) \), and the near end at a distance of \( \frac{1}{2}(t_{3}-t_{2})\), so they must take the length, in light-seconds, to be
\begin{equation} L = \frac{1}{2}[(t_{4}-t_{1})-(t_{3}-t_{2})] \end{equation}Now, by the definition of k, from "the rod's perspective" (you can imagine somebody holding the rod outstretched in front of them if you wish), the first pulse crosses the end of the rod nearest the observer sending the light pulses at \( t_{1}' = k t_{1} \), and returns to the near end at \( t_{2}' = \frac{t_{4}}{k} \). According to "the rod," the time difference \( t_{2}'-t_{1}' = \frac{t_{4}}{k} - k t_{1} \) must be twice the time it takes the radar pulse traversing the rod to reach the rod's far end, and thus, in light-seconds, the rod, in its own (rest) frame is
\begin{equation} L_{0} = \frac{\frac{t_{4}}{k} - k t_{1}}{2} \end{equation}Combining (1)-(4), it can be shown that
\begin{equation} L_{0} = \frac{k^2+1}{2k}L \end{equation}That is to say, given that we measure via radar a length L, we know that its "true" rest length \( L_{0} \) is given by (5).
Inverting this relationship, and remembering that the observer using radar can only say that the rod moves at \( v = \frac{k^2 - 1}{k^2 + 1} \) light-seconds / second, we have
\begin{equation} L = L_{0}\sqrt{1-v^2} = \frac{L_{0}}{γ} \end{equation}This is the special-relativistic phenomenon known as length contraction. We can also see that the radar reflections are not simultaneous in the frame of reference of the rod: the first reflection happens at \( t_{r1}' = \frac{\frac{t_{4}}{k} + k t_{1}}{2} \), and the second at \( t_{r2}' = k t_{2} \).
It turns out, after some algebra, \( t_{r1}' - t_{r2}' = - v L_{0} = -γ v L \), i.e. the event of the radar reflection of the far end of the rod happens earlier than the event of the radar reflection of the near end of the rod, whereas the reflections were, by construction, simultaneous in the frame in which the radar pulses were sent.
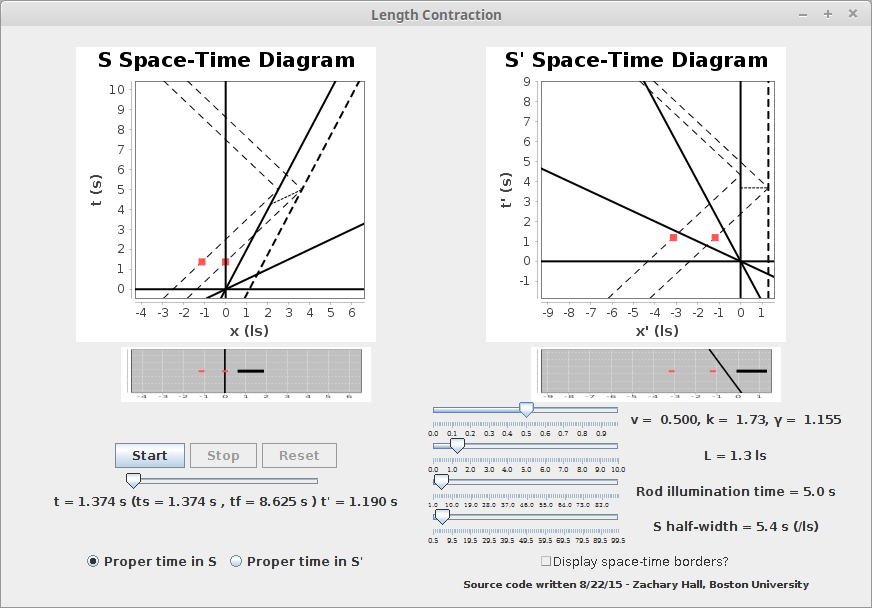
This thought experiment is exactly what is shown, in a user-interactive way, by the application LC.jar:

Note that, in this application, the rest length of the rod is called L rather than \( L_{0} \) for ease of display.
Time is plotted on the vertical axis and the line of three dimensional space along which there is relative motion on the horizontal axis from the perspective of both the observer sending the radar pulses and of the rod in what are called space-time diagrams. Since the units are set to seconds and light seconds, light pulses are situated at 45° angles in these diagrams, while moving observers are constrained to lines "more vertical" than 45°, an observer at rest in a frame of reference being drawn as a vertical line. In this application, the steep black line in the S Space-Time diagram is the near end of the rod, and the parallel dashed line the far end of the rod. Both are being measured simultaneously by the two reflecting radar pulses shown. A dotted line shows the half-way point of the times of the near end of the rod first recieving the first radar pulse and then later recieving the reflection of this pulse, showing the non-simultaneity of the radar reflections according to the rod (a phenomenon to be more explicitly explored by the next application). The whole process of measurement is shown in both the space-time diagram of the observer sending the radar pulses (S Space-Time Diagram) as well as that of the rod (S' Space-Time Diagram) and projected into what this "looks like" for a given time (looks like is not quite right, because we see with light, and here we are mapping the where light itself is as a function of time).
The user can then animate this process of measurement, and choose to set the system time to either the time according to the observer sending radar pulses (Proper Time in S), or to the time according to the rod (Proper Time in S'). If the former is selected, the animation shows consistency in the crossing of the radar pulses of the rod's Space-Time x'=0 line, i.e. where the near end of the rod is, for both frames; if the latter is selected, the animation shows consistency in the crossing of radar pulses for the observer's Space-Time x = 0 line, i.e. where the observer is, for both frames. This comes from the definition of time dilation, which is a relation between the ascribed times of events along observers' x = 0 and x' = 0 lines. The time can then be started and stopped with the start and stop buttons, reset to the beginning with the reset button, or, if the time is paused, the user can "slide through" time, to concentrate on particular times of interest, e.g. just as the radar pulses are reflecting.
The user can then freely adjust the k value (and hence also relative velocity v and γ), the rest length of the rod (here called L), when the rod is "illuminated" by the radar pulses according to the observer in S, and the half-width of the S Space-Time diagram, with the S' Space-Time Diagram axes automatically selected to be the same scale as the those of the S Space-Time diagram and to include the times of radar reflection.
The user can also choose to display "space-time borders" in both frames, which are the outlines of what the S Space-Time region shown maps to in the S' Space-Time diagram and vice-versa, as shown in the next image. This will become more clear with explanation of the next two applications.
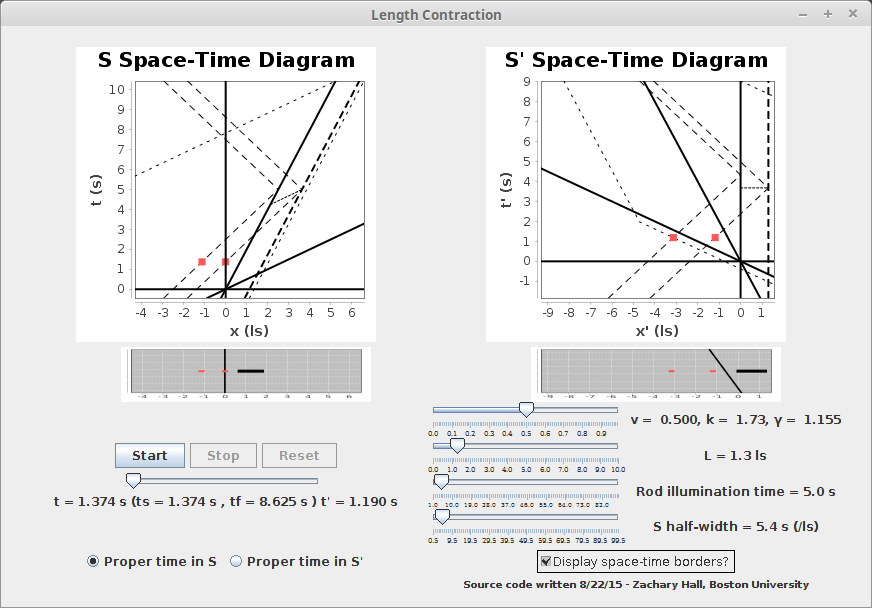
Remember that there is nothing special about the frame of reference of the observer holding the radar gun. We simply at first imagined things from this perspective to help build intuition, but this exact same argument could apply to an observer riding along with the rod -- if they had measured the other observer (at rest in the S frame) with their own radar gun, they would measure the S observer themselves to be length contracted in exactly the same way as shown above.
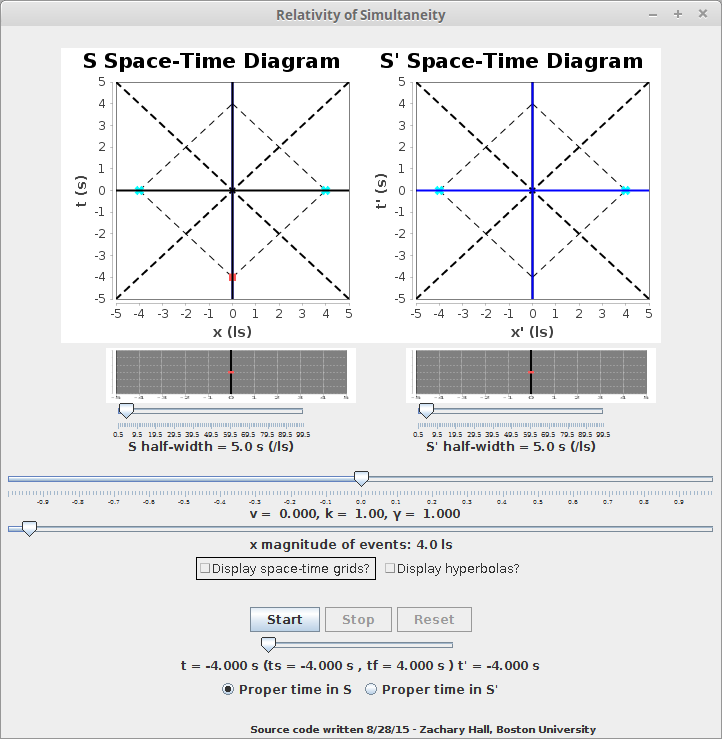
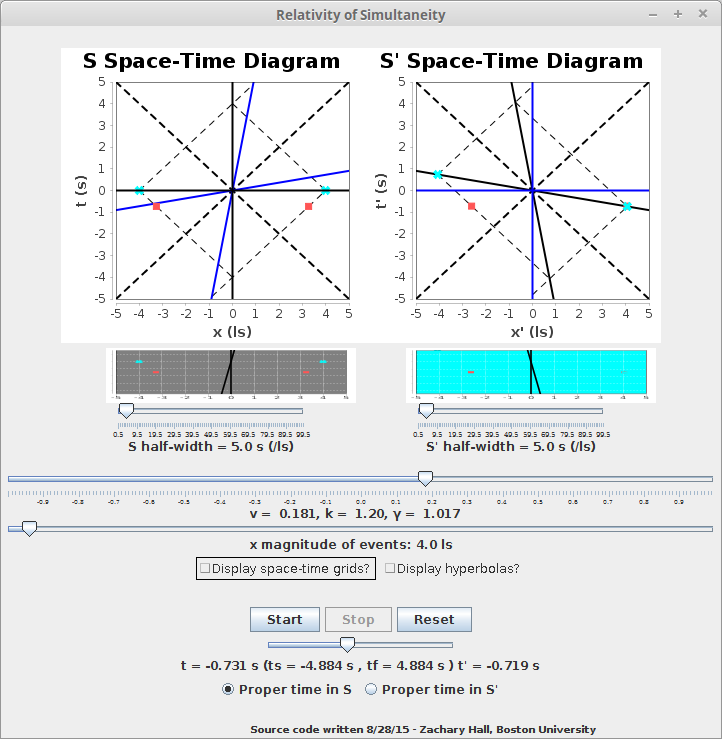
Now we look in more detail, with the assistance of another visualization application and thought experiment, at the relativity of simultaneity encountered in the above discussion. Consider two events, according to some observer -- call him Aeolus -- occurring at t = 0 at equal and opposite distances (along some line of space) as determined by Aeolus. How would he determine that these events occurred at this time? By the same radar technique used to measure a moving rod. He would have to send out radar pulses in opposite directions, towards these events at some time \( t = -t_{0} \), and would receive them back at \( t = t_{0} \). Then, he would say that the events occurred at \( t = 0 \) and were \( d = ± t_{0} \) light-seconds away, or, in conventional units, \( d = ± ct_{0} \), as this is half the round trip time of the radar pulses to reach and reflect off the events. We may as well think of the reflections as the events . This process is shown (redundantly with two space-time diagrams) below:
Now consider again an observer moving with respect Aeolus and coinciding in location with him at t = 0 -- call him Hermes. Then, in order to measure the times of the distant events, Hermes must send out radar pulses at appropriate times for the radar pulses to reflect off the same events -- that is to say, in order to be the same reflection. In order for the reflections to be the same, the radar pulses sent by Hermes must coincide with those of Aeolus. Thus, in order to reflect off the same event, Hermes must send out the radar pulse towards the event towards which he is moving earlier (according to his clock) than does Aeolus according to his clock, and will receive it back earlier as well. By symmetry, the converse is true for the event away from which Hermes is moving. This is all made much clearer by the below screenshot of RELSIM.jar:
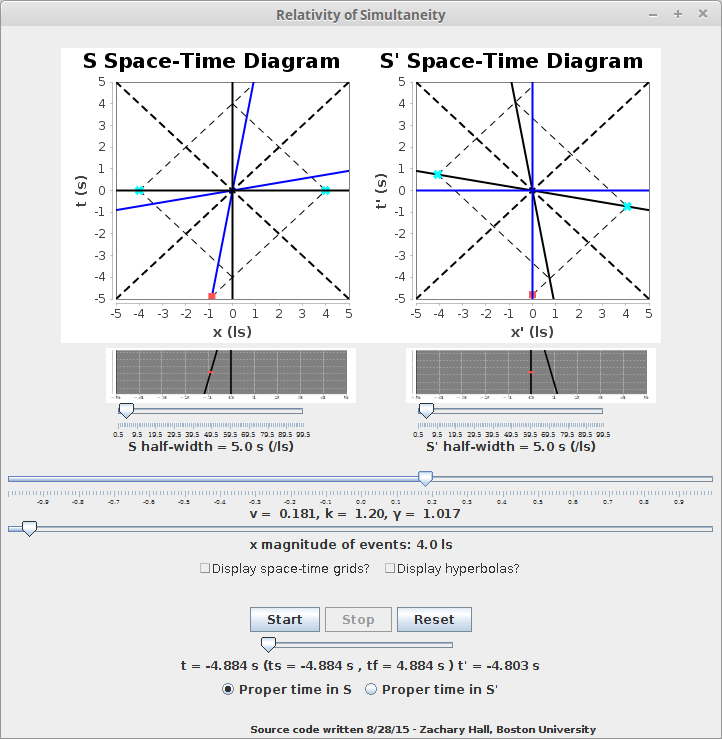
Quantitatively, by the k-calculus, in order to reflect off the event towards which Hermes is moving (the event on the right of the screen above), Hermes must send out the radar pulse at \( t_{1}' = -k t_{0} \), and will receive it back at \( t_{2}' = \frac{t_{0}}{k} \), and thus will say the event occurred at
$$
t_{r}' = (-k + \frac{1}{k})\frac{t_{0}}{2} = \frac{-k^2 + 1}{2k} t_{0} = - \frac{(k^2 - 1)}{2k} t_{0} = - \frac{k^2 -1}{k^2 + 1} \frac{k^2 + 1}{2k} t_{0}.
$$
In units in which c = 1 (seconds, light seconds), this is \( t_{r}' = -vγd \). In conventional units, \( v → \frac{v}{c} \) and \( t_{0} → \frac{d}{c} \) and we have \( t_{r}' = -γ\frac{vd}{c^2} \). For the event away from which Hermes is moving, he must send out the radar pulse at \( t_{3}' = -\frac{t_{0}}{k} \) and will receive it back at \( t_{4}' = k t_{0} \), and thus will ascribe to it a time of \( t_{l}' = (k - 1/k)\frac{t_{0}}{2} \), which is exactly the negative of \( t_{r}' \). Thus with c = 1, \( t_{l}' = vγd \), and in conventional units \( t_{l}' = γ\frac{vd}{c^2} \).
There is certainly nothing special about the particular distance at which the distant events occurred, and so we may abstract from this a general relationship of relativity of simultaneity, for observers moving with respect to each other and coinciding in location and time at t = t' = 0, that for the observer moving with respect to the observer for whom the events are simultaneously occurring at t = 0, the events will happen at a time \( t' = -vγx\) or \( t' = -vγ\frac{x}{c^2} \) (again depending on choice of units), where x is the signed distance of the events as determined by the observer for whom they are simultaneous (Aeolus) and v is the signed velocity of the relatively moving observer (Hermes) -- if v and x are of the same sign, the events happen earlier, while if v and x are of opposite sign, the events happen later. When deriving the above expressions for \( t_{r}' \) and \( t_{l}'\), we said that Hermes was moving towards and away from the two events, respectively. But Hermes is only moving towards and away from those events according to Aeolus -- as far as Hermes is concerned, he is at rest with respect to those events. Indeed, this is crucial to our assertion that Hermes will say that the events are non-simultaneous -- if he somehow knew he were "really" moving with respect to the events, he would correct for this in his calculation of when and where the event takes place, and arrive at the same answer as Aeolus.
What we have really seen is that, owing to the fact that the only meaningful determination of distance and time we can give is with radar signals, or more generally with electromagnetic radiation (visible light included), the only notion of simultaneity of events we can give is observer dependent.
We can say a bit more if we consider a set of processes, say a solid object (a solid object is, at bottom, a collection of many, many quantum-mechanical processes). Consider that this object, i.e. set of processes, is at rest with respect to Aeolus, and Aeolus measures the place and time of
some event (i.e. subset of the processes comprising the object) to be at (x,0). Now consider that Hermes is moving towards this set of processes (or, equivalently, that this set of processes is moving towards him), and measures the place and time of that same event. Then that same event, which is to say that same subset of the processes comprising the object, will be determined to happen at \( t' = -vγx\). This is shown below, with the assistance of the final application, to be introduced shortly:
We can see that the places and the times of the events comprising process differ for the two observers (as opposed to differing only in places, as assumed by all physics prior to Special Relativity), and that the set of processes is time dilated with respect to the observer moving relative to the set of processes (Hermes), as we have already predicted from the introduction of the k-calculus.
The user can explore this relativity of simultaneity in RELSIM.jar by adjusting relative velocity, the magnitude of the events' separation for the observer for whom they are simultaneous (the S observer in this application), and the half-width of the two space-time diagrams. Again, the user can animate this process of measurement, which is projected for both observers onto a graph what it "looks like" at a given time, choosing which observer's proper time to set the system time to agree with, the other observer being time dilated from this perspective. As a visual aid, the projected animation's background flashes blue whenever a radar reflection happens according to the observer:
Remember, though, that we observe the world with light , and so what you are seeing is really just a tool for imagining logical consequences of the postulate that the speed of light is the same for all observers (actually, this is itself a logical consequence of the postulate that the speed of light is independent of the velocity of its source), and not anything you could actually observe yourself, as what is shown is the path light itself follows through the spacetime.
Be careful not to ascribe a privileged position to the S observer, for whom the events are simultaneous. This does not mean that events "really are" simultaneous in this frame -- this is a matter of choice. We have asked "given that some observer determines two distant events to be simultaneous, when will an observer moving with respect to this observer determine these events to happen?" We could have just as easily made the observer for whom the events are simultaneous the S' observer in the animations, and we would see the same information, as we have allowed the relative velocity in the application to range from - c to c (-1 to 1). Just as with length contraction, this effect is a reciprocal, relative effect resultant from the only manner in which an observer can determine times of events, and not an absolute effect of a failure of some observer to measure the "true" simultaneity of events.
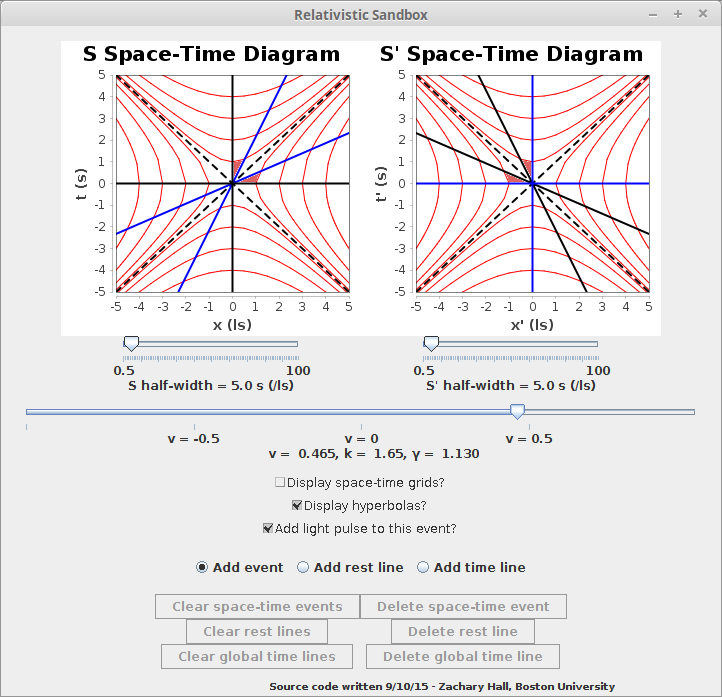
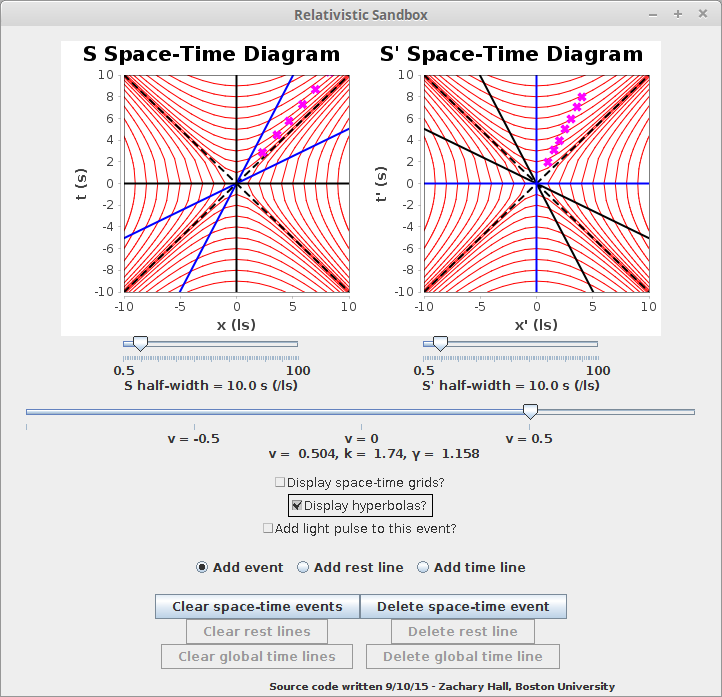
Two additional features are apparent: "Display space-time grids?" and "Display hyperbolas?". Checking the first displays the entirety of how the places and times of events in the S frame map to the S' frame:
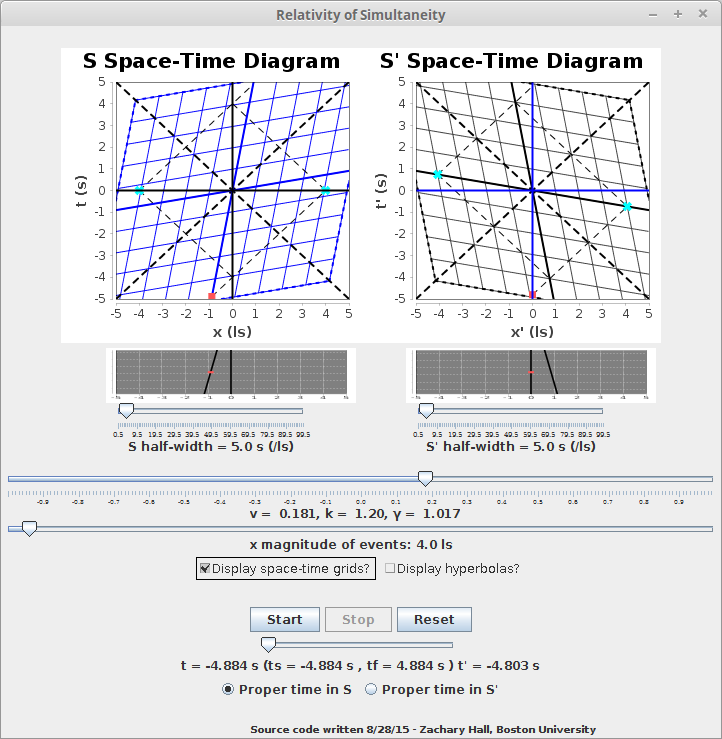
Imagine a rectangular, regular grid marking every second in the S frame and every light-second of separation on the S-frame. This is what is mapped to the "squished square" or rhombus-type grid in the S' Space-Time diagram. The converse is true for the rhombus-type grid in the S Space-Time diagram. I hope that enough intuition has been built that this seems at least plausible to the reader. It will be more rigorously and intuitively demonstrated with the final application. The "X" pattern of dotted lines about the origin of both space-time diagrams are light pulses arriving at and leaving the observers at t = 0, and define what are called the observers' light cones. This, too, will be further explained with the final application.
Checking the "Display hyperbolas?" displays what are called Minkowski hyperbolas, which represent space-time events with what is called constant proper distance or with what is called constant proper time:
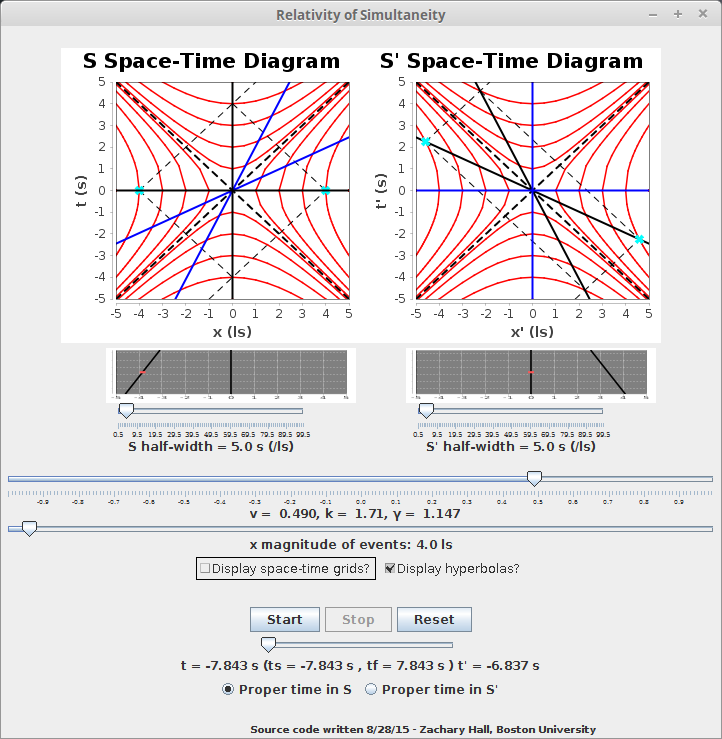
You can see that the events marked in this particular application are on the same hyperbola for both observers, regardless of velocity, and thus, since they are the same events, these hyperbolae define where the events most meaningfully reside in the spacetime. That the timelike hyperbolae serve the same function will be demonstrated by the final application.
We are now ready to generalize the relationship between space-time coordinates for relatively moving observers coinciding at (t,x) = (t',x') = (0,0). To do so, we must generalize the process of radar measurement of an event, or of assigning space-time coordinates to radar reflections, as has been so far described. To do this, we need merely say that some observer in the S frame sends out a radar pulse at time t - x and receives it back at time t + x, so that the event is ascribed coordinates (t, x) in the S frame (x here measured in light-seconds), and that the observer moving relative to the S observer, in frame S', sends out a radar pulse at time t' - x' and receives it back at time t' + x', such that this radar pulse coincides with the one sent out by the observer in S, so that the observer in S' ascribes coordinates (t',x') to the same event, or same radar reflection, as that said to happen at (t,x) in frame S. By the k-calculus, in order for these radar pulses to coincide, it must be that
$$ t' - x' = k(t-x) $$This will become more clear when the application is actually introduced.
With a little algebra, it can be shown that
$$ t' = \frac{1}{2k}(t+x) + \frac{k}{2}(t-x) = \frac{k^2 +1}{2k}t - \frac{k^2 - 1}{2k}x = \frac{k^2 +1}{2k}t - \frac{k^2 -1}{k^2 + 1}\frac{k^2 +1}{2k}x $$In units of seconds and light-seconds, this becomes
\begin{equation} t' = γ(t - vx) \end{equation}whereas in conventional units
\begin{equation} t' = γ(t - \frac{vx}{c^2}) \end{equation}as \( x → \frac{x}{c} \) and \( v → \frac{v}{c} \). This is called a Lorentz Transformation -- specifically, a Lorentz boost along x.
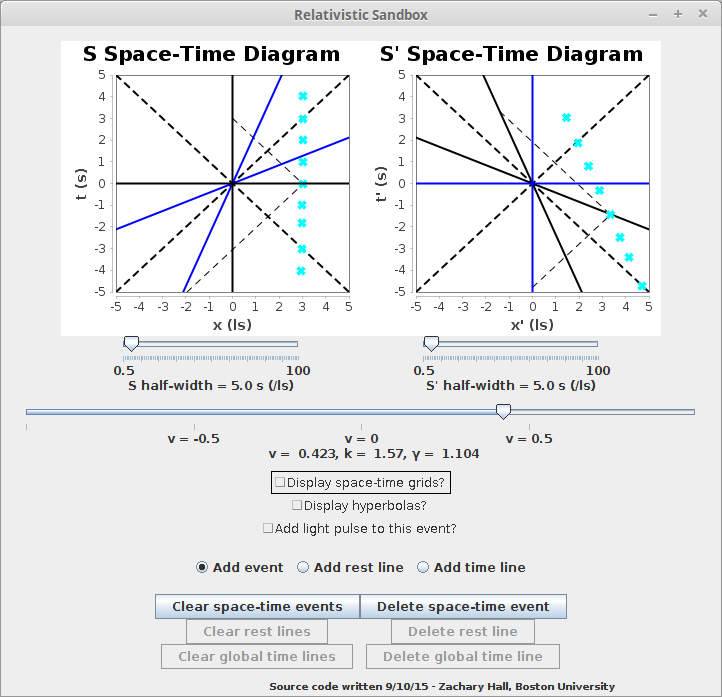
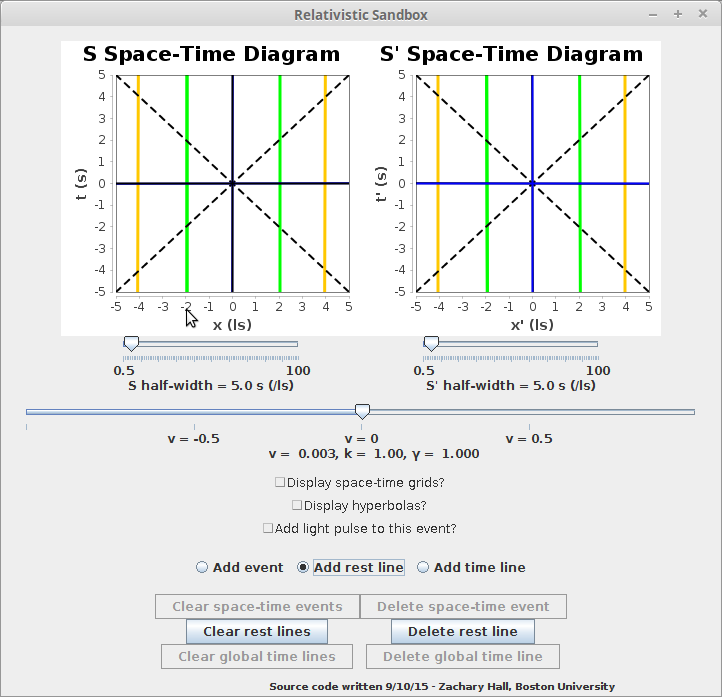
The relativistic sandbox -- SANDBOX.jar -- allows the user to visualize exactly the above reasoning for any such event by specifying an event that has fixed space-time coordinates in one frame:
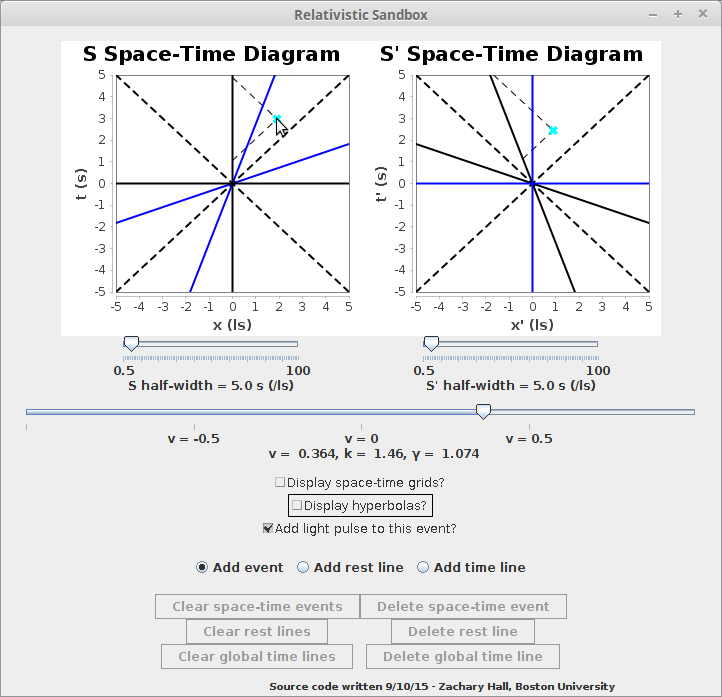
Of course, there is nothing special about one frame of reference over another, so the user may also specify events that have fixed space-time coordinates in the other frame:
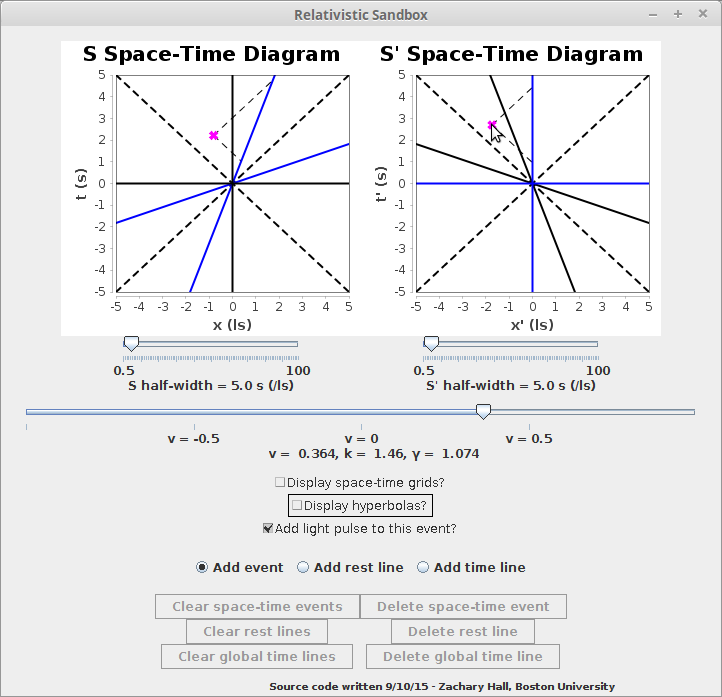
The user can specify whether or not to connect the specified event with "light pulses" (partial null cones), can add any number of such events, and can delete the events in the reverse sequence in which they were added, or all at once. The user can also add the space-time grids which map the S space-time coordinatizations to the S' diagram and vice-verse, as in RELSIM.jar, and the specified events will be appropriately transformed:
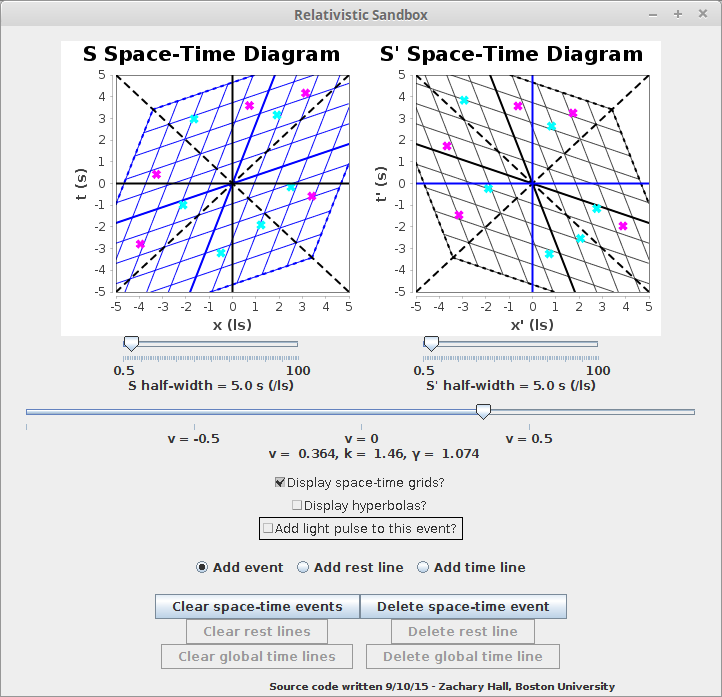
The user can also add Minkowski hyperbolas, which the user can now confirm serve as the invariant characterization of the space-time coordinates of any event. That is to say, if an event is on a hyperbola in one frame, it will be on the same hyperbola in any frame moving with constant velocity with respect to that frame. Along these hyperbolae, the value \( t^2 - x^2 \) is a constant, or, in conventional units, \( t^2 - (\frac{x}{c})^2 \) is a constant. This can be shown mathematically to be true of the Lorentz transformations -- the quantity \( t^2 - x^2 \), or \( t^2 - (\frac{x}{c})^2 \) of any event for an observer in a certain inertial reference frame is preserved by any such transformation.
We are also ready to abstract another concept. What is it that we've been doing when we say that an event's place and time is determined by radar measurement? We have been considering that an observer sends an electromagnetic pulse to some change in the universe and receives one back from that event. This is just the same as saying the event is connected to an observer by electromagnetic radiation prior to that event and after that event. This connecting of the event into the past and the future happens along the future and past light cones , also known as null cones of that event. The past null cone is defined as the totality of space-time paths which electromagnetic radiation from the past could have taken to have arrived at an event, and the future null cone is defined as the totality of space-time paths electromagnetic radiation can take when leaving the event. With this terminology, we can now say that the places and times of events are determined by the intersection of the world-line of some observer with the past and future null cones of those events, where a world-line is the collection of places and times of an observer.
As the user can experiment in the application, events lying outside of the null cones are subject to the relativity of simultaneity -- their temporal ordering w.r.t. the event (t,x) = (t',x') = (0,0) can be swapped or made to be simultaneous by an appropriate choice of reference frame, while events inside either the future or past null cones have a temporal ordering that all observers who are coincident at (t,x) = (t',x') = (0,0) agree upon. Thus, the interior of the past null cone is oftentimes said to be the absolute past , the interior of the future null cone the absolute future , and everything else the present , relative to the space-time event of the intersection of the two hypothetical inertial observers.
There are limitations to this user-interactive application. Everything shown holds for observers who have synchronized clocks and are at the same location at t = 0, but it must be remembered that, as far as our experience permits us to know, everything in nature has no choice but to march through time, so to speak, and this application can only serve to visualize the possible past, present, and future relations of space-time events for classes of inertial observers coinciding at one place and at one time. However, it can be used to get a feel for the general chronogeometric structure of Minkowski spacetime.
For an example of a more realistic demonstration of how events in the spacetime can be characterized by an observer moving through space and time and taking their past and future null cones with them, see this GIF from Wikipedia:
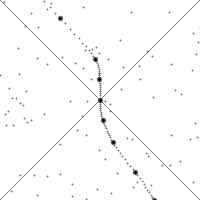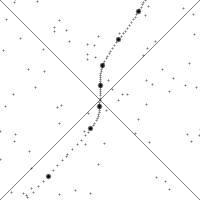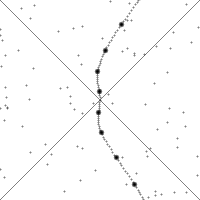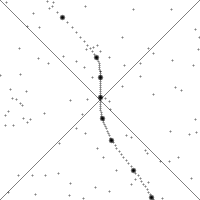
A variety of thought experiments can be visualized with the above application. Take, for example, the so-called barn-pole paradox, wherein some observer is carrying a pole and running at a speed that causes all objects in the direction this observer is moving to be length contracted to half their rest length. Call this observer Hecate.
Now consider that Hecate's pole is, when at rest, i.e. as seen by Hecate, twice the length of a barn when it is at rest, with open doors on both ends, towards which Hecate is running. Then, according to an observer in the center of the barn and at rest with respect to it, -- let us call this observer Proteus --, by the symmetry of length contraction, the pole, and Hecate, will appear to be half their rest lengths along the direction of relative motion and thus the pole and the barn will appear to be the same length. Now consider that a button is wired to a mechanism to close both the doors "instantaneously" and simultaneously, which Proteous presses such that the two doors close at the moment when the pole just fits into the barn. But from the perspective of Hecate, it is the barn that is length contracted, and thus appears to be one fourth the size of the pole! Won't then, according to Hecate, the two doors collide with the pole, which never fits into the barn all at the same time? According to Proteus, it seems, then, no collision occurs, while according to Hecate, one does. Certainly renaming places and times of events cannot determine the physical events occuring. So what is happening? The crux of the paradox can be seen in a careful examination of what we mean when we say "at the same time." We have already seen that the two observers differ in their notions of what happens at the same time at a distance -- and the pole's two ends are certainly a distance from Hecate. Let us see what the application has to show us.
We first set up an 8 light-second long pole at rest with respect to a 4 light-second long barn (this is a large pole and a large barn -- the Earth-Moon separation is about 1.3 light-seconds). Imagine that the two barn doors are always left open so that the pole is physically permitted to be there:
We then consider the case where the observer holding the center of the pole (Hecate) and observer in the center of the barn (Proteus) still coincide at t = 0 (as all classes of observers must in this application), but where there is relative motion such that \( γ \approx 2 \) and, to the user's eye, the pole momentarily fits inside the barn in frame S. We then mark the momentery coincidence of the barn door frames and the pole ends (according to the observer in the barn) with events that represent instantaneous closings of the doors in the frames with events having their own null cones:
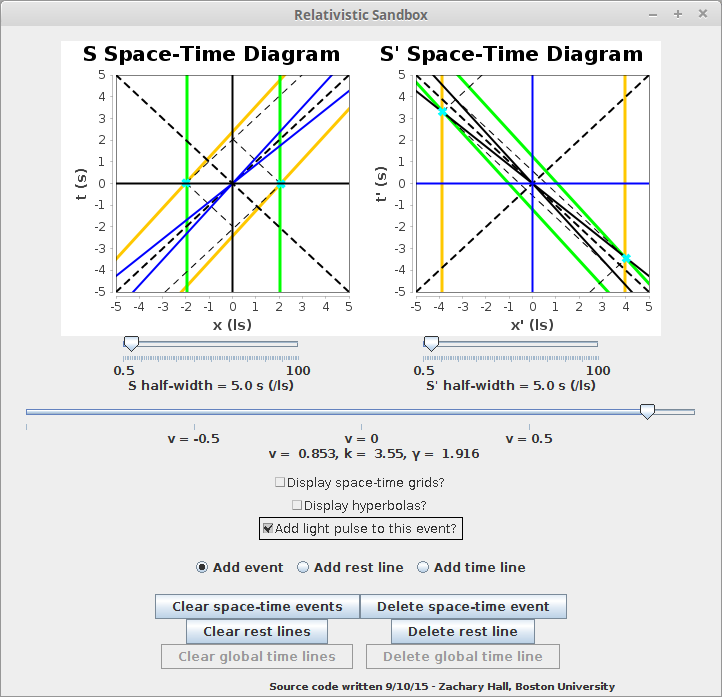
As we can see, these two events of the closing of the two ends of the barn doors that were simultaneous for Proteus happen at different times for Hecate -- the event of the door closing at the far end of the barn towards which Hecate was running happens earlier than the event of the door closing at the near end. ("Far" and "near" refer to the relative positions of the runner and the two doors before the pole has entered the barn ( t < ~ -5 s), i.e. "far" is on the right of the space-time diagrams above, "near" on the left.) Referencing the space-time diagrams, we can see that this assignment of times by Hecate was just what was required by our considerations of time in RELSIM.jar. Referencing equation (7), we see that in the case where γ = 2, then \( t_{far}' = -2\sqrt{3} \) s \( \approx -3.46 \) s and \( t_{near}' = 2\sqrt{3} \) s \( \approx 3.46\) s, which agrees with the shown S' Space-Time diagram.
But something still seems amiss to our intuition, or, at least, something did to mine for a while. To retrain our intuition, consider how the observer in the barn knows that he pushed a button that caused the two doors to close at the same time. This observer couldn't have affected the doors instantaneously -- in Special Relativity, no signal can travel faster than the speed of light, which would take a finite time to reach the doors. The signal sent through the button was ultimately a current through the wires connecting the button to the doors. A current is really driven by what is called an electric field in the conducting material of the wire. It turns out, that, after applying our relativistic understanding of space, time and causality to electricity, we conclude that, in a region of space-time previously absent of an electric field, an electric field can only be "set up" at the speed of light. Thus, signals travelling from the center of the barn (the button pressed by Proteus) to the two doors travelled at the speed of light -- more abstractly, they propogated along the null cone of the button pressing event in the space-time. In the S Space-Time diagram, this is at (t,x) = (-2 s, 0 ls). Further, Proteus would only know that he was successful in making the barn doors close "at the same time" (i.e., that both the button and the wires weren't faulty) when he sees them close at the same time. This, of course, was the final result of a process of electromagnetic propogation of light; it happens in the S Space-Time diagram at (t,x) = (2 s, 0 ls). Thus we see in this case, too, that the successful causing of two distant events to happen "at the same time" and the knowledge that they indeed did happen "at the same time" is dependent on the null cone causal structure of Minkowski spacetime.
Consider now that the button Proteus used was faulty and never did communicate the signal via electric fields through wires to the doors to close, and that instead, it was really Hecate running with the pole who caused the doors to close "at the same time" as determined Proteus. Proteus would certainly make such a determination if he were oblivious to the fact that the button was faulty, and really thought that electric fields were being communicated through the wires and causing the doors to close, and nonetheless observed (with light, of course) the two doors close "at the same time" at (t,x) = (2 s, 0 ls) (that they "actually" closed at (t,x) = (0 s, +/- 2 ls) is then inferred from this observation and that he pressed the button at (t,x) = (-2s, 0 ls)). How then, would Hecate cause such a transpiring of events and trick Proteus into believing he had a functioning button? Certainly she didn't press a functioning button of her own at the same place as Proteus's faulty button -- she wasn't at the same place as Proteous when he pressed his faulty button. This is the case no matter who determines what when and where mean, for it is a statement about causal relations, which all observers agree upon. This can be checked on the above space-time diagrams.
Consider that the mechanism causing the doors to close was actually a radar-sensitive receiver, and that Hecate sent out radar pulses at strategic times (according to her watch) at the receivers such that Proteus was so tricked. How would Hecate do this? Clearly she would want the electromagnetic pulses of the radar to coincide with where the electric field of the wires would have been on their way to telling the doors to close. To do this, Hecate would need to send out the pulse towards the far door a bit earlier than if she were at rest, so they appear to leave the faulty pressed button as it is pressed (I say appear because the radar gun is really the efficient cause of the pulse), and would need to send the radar pulse towards the near end of the door when she would have first observed the electric field in the wires of the faulty button, had that button not been faulty. Further, Hecate would receive the light telling her that the far door closed earlier than if she were at rest with respect to the doors and would receive the light telling her the near door, now behind her, closed later than if she were at rest with respect to the doors. These two factors combined, that she both needed to act at earlier times to cause the process towards which she was moving (the closing of the far door) and perceived it earlier than if she were at rest with respect to that process, would lead Hecate to say that the far barn door must have closed earlier than the near barn door.
This is precisely what is shown in the above pair of space-time diagrams -- the partial past null cones of the events represent either the electric field in the wire or the radar pulses, and the partial future null cones represent the transmission of information about those events to Hecate and Proteus (S and S' Space-Time diagrams). Note that you cannot even see when Hecate had to send the first pulse nor when she saw the near door close on the space-time diagrams above. Zooming out shows when these occurred:
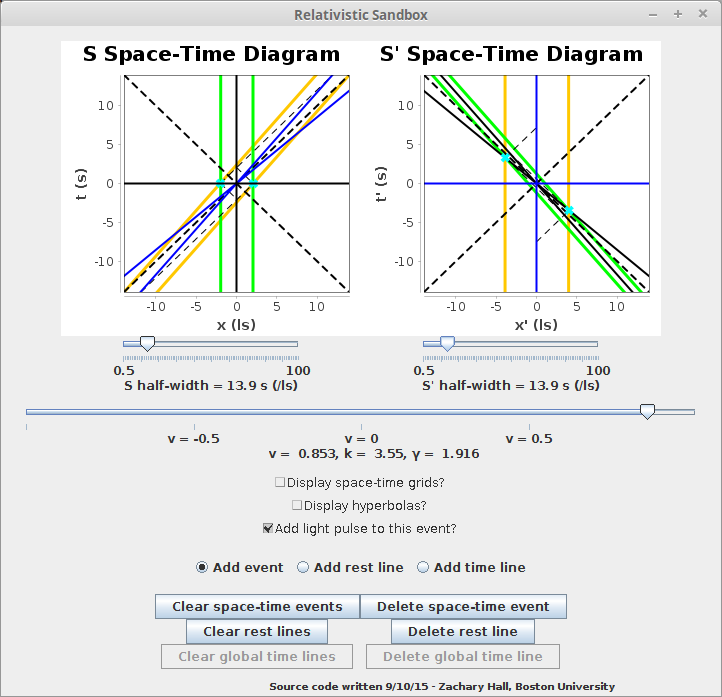
Another special-relativistic phenomenon that is easy to visualize with this application is the relativistic doppler shift. Our study of light, electricity, and magnetism has revealed that light is actually a particular class of what are called electromagnetic waves, oscillating with a certain frequency and propagating along the null cones. See this image from Wikipedia commons:
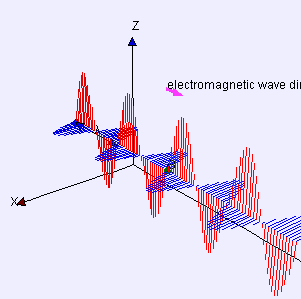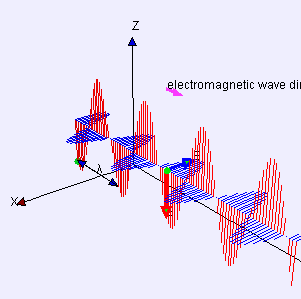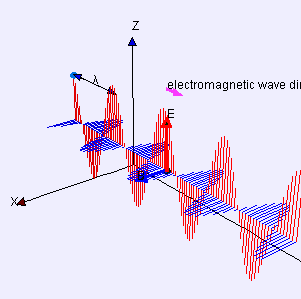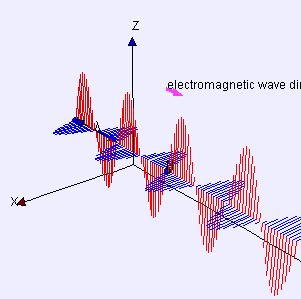
What actually generates this radiation is oscillating charges, and it is the frequency of this oscillation that determines the frequency of the waves, and the frequency of the waves received is what gives them their physical properties in which we are generally interested. For example, the physical mechanism causing us to perceive the color red (ignoring psychological, physiological, and philosophical questions about perception for our purposes) is in response to a characteristic frequency of the electromagnetic waves comprising what we call red light. Thus, we can think of the "color" of a more general electromagnetic wave as corresponding to its physical property of frequency. Consider an electromagnetic wave of the frequency of 1 Hz (1 cycle of the wave generated every second). This is radiation of very low frequency -- low frequency radio waves are about a thousand times faster in oscillation than this. Nonetheless, we choose a simple number for the sake of ease of imagination. This means that, for the observer generating the radiation, a complete oscillation of source charge happens once per second, and the maxima of the waves are received once per second by an observer at rest with respect to the oscillating charge generating the radiation. We can draw this process of charge oscillation by marking events along an observer's world-line every 1 second:
Now consider an observer moving with respect to the oscillating charge. The maxima of the waves are now mediated along null future cones connecting the events corresponding to the genesis of the maxima of the waves, in the oscillating charge's frame. Observing this process on the space-time diagrams by changing the relative velocity shows us the relativistic blue shift as the temporally compressed series of receptions of the maxima of the electromagnetic waves before the relatively moving observer passes the oscillating charge and the relativistic redshift as the temporally extended series of receptions of the maxima of the electromagnetic waves after the relatively moving observer passes the oscillating charge. This determines the effective frequency of the radiation as measured by the relatively moving observer. As can be seen, the redshift and blueshift magnitudes are determined by two factors: 1) the relatively moving observer has moved with respect to the charge between every successive generation of a maxima in the wave and 2) in order for the radiation itself to move along the null cones of the spacetime, the events in the oscillation of the charges corresponding to the genesis of the maxima are time dilated for the relatively moving observer, as demanded by our earlier considerations of the nature of time.
I now explain what I mean by "chronogeometry" and what the chronogeometry of Special Relativity is. We have seen that all motion is really motion through a spacetime, where the amount by which a process moves through time depends on the route through the spacetime that process takes. Just as different paths through traditional Euclidian three-space have different lengths (the straightest path between two points being the shortest such path), different paths from one spacetime point to another have different lengths in time. The assertion that the straightest paths in Euclidian geometry are the shortest is, at bottom, dependent on Euclid's postulates -- i.e. we assume that the relations of points in three-dimensional (Euclidian) space really are such that the straightest paths are the shortest, and are characterized by the line-element expression \( dσ^2 = dx^2 + dy^2 + dz^2 \). Similarly, the spacetime of Special Relativity is built upon the postulate that the speed of electromagnetic radiation is independent of the velocity of its source -- we have explored some of the logical consequences of this postulate; it turns out that they and others can be understood as manifestations of an alternative sort of "time-involving" geometric structure, or a chronogeometry. The chronogeometric nature of Minkowski spacetime can be visualized by invoking the geometric idea of a hyperbolic angle, which is closely connected with our traditional idea of angle, differing in that we consider a unit hyperbola instead of a unit circle. It is best explained visually:
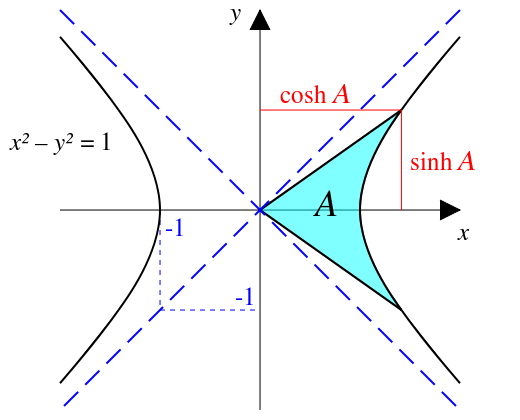
In the above image, the area shaded A is the hyperbolic angle, with the so-called hyperbolic cosine and sine defined as the segments so drawn for a unit hyperbola -- defined by the expression \( x^2 - y^2 = 1 \). If the hyperbola is a more arbitrarily defined by \( x^2 - y^2 = b^2 \), then they are defined as the ratio of the segments drawn above to the value b. The hyperbolic tangent is defined analogously to the circular tangent, \( \tanh A := \frac{\sinh A}{\cosh A} \). Referencing the space-time diagrams, it can be seen that the inverse "slope" of the world-line of an inertial observer corresponds to v in units with c = 1 and to \( \frac{v}{c} \) in conventional units, as time is drawn vertically. It can also be seen that this inverse slope is exactly what \( \tanh A \) is, where A corresponds to the area shaded below:
In Special Relativity, we give this quantity A such that \( \frac{v}{c} = \tanh A \) the name rapidity. It is denoted by various symbols -- the Greek letter Φ or the letter "w" for example. It can then be seen visually that the quantity \( γ = \cosh A \) is the time-dilation factor, determined by the ratio of how long one second in an observer's rest frame takes in the frame of reference in which that observer is moving -- comparing our space-time diagrams, remembering that events that start on hyperbolae stay on those same hyperbolae, with the visual definition of rapidity, we see that this is precisely \( \cosh A \). It follows that \( \frac{v}{c} γ = \tanh A \cosh A = \sinh A \), and thus we may re-write the a boost along x as
Thus the class of Lorentz transformations considered here -- boosts along the so-called x direction -- can be thought of as hyperbolic rotations of spacetime coordinates.
Using the definition of rapidity, we can easily derive the formula for the relativistic collinear addition of velocities, i.e., if observer A measures an object to be moving at v along the x direction, and observer B measures observer A to be moving at u along the x' direction (x' because it is in a different spacetime coordinate system, but we are considering the same line of space), at what velocity will observer B measure the object to be moving? The statement that observer A measures the object going at v along x is a statement that, by the radar technique discussed, observer A measures a series of places and times of the events comprising the object such that \( \frac{dx}{dt} = v \). For simplicity we can consider the case that at t = 0, the object was at x = 0 (as was observer B), giving a worldline of the object of \( x(t) = vt \) in observer A's spacetime coordinate system. Remembering the definition of rapidity, this can also be written as \( x(t) = ct\tanh{A} \) where A is the rapidity of the object in the A frame. Since it is said that observer A moves at velocity u along the x' direction relative to observer B, if we define the relationship \( u = c\tanh{B} \), we must hyperbolically rotate the spaces and times of the worldline of the object in frame A by a hyperbolic angle -B (minus because observer B moves at -u w.r.t. observer A), i.e. we must transform \( x(t) = ct\tanh A \) with
Carrying this out gives
and thus
Thus observer A will measure the object to move at
This is the formula for the collinear addition of velocities, and it was found by Lorentz transforming the spaces and times of the events comprising a worldline characterized by a particular velocity / rapidity in a particular inertial reference frame. The reader can check that if the same analysis is performed directly with equations (9) and (10) without ever defining rapidity, the same result is reached. It is a geoemtric identity that
and thus the rapidity C of the object in the B frame, defined by \( \frac{v'}{c} = \tanh C \) is such that \( \tanh C = \tanh(A + B) \), and thus, C = A + B. This shows that successive collinear boosts are successive hyperbolic rotations of spacetime coordinates of a worldline .
We can show this process in the relativistic sandbox by first marking a series of events corresponding to an observer moving at constant velocity, say at v = 0.5c :
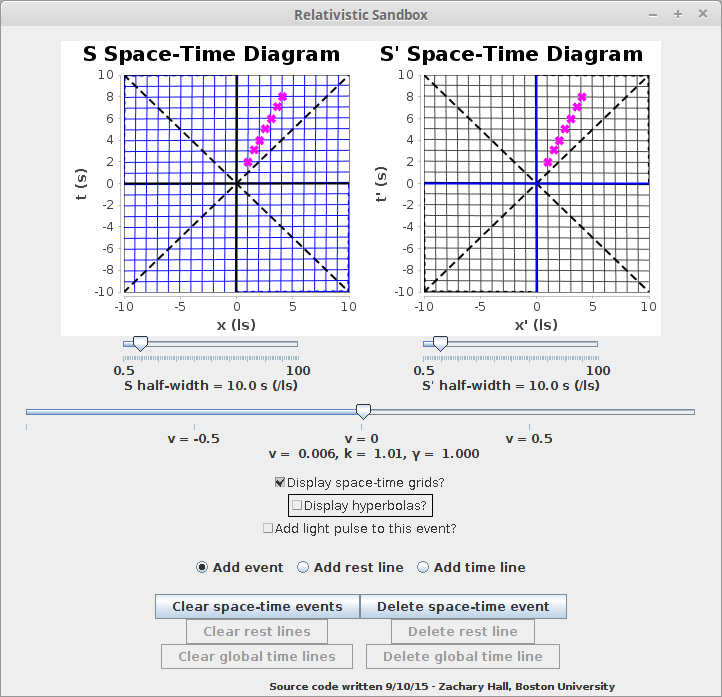
We can then boost this into a frame moving at u = -0.5c with respect to the originally considered frame:
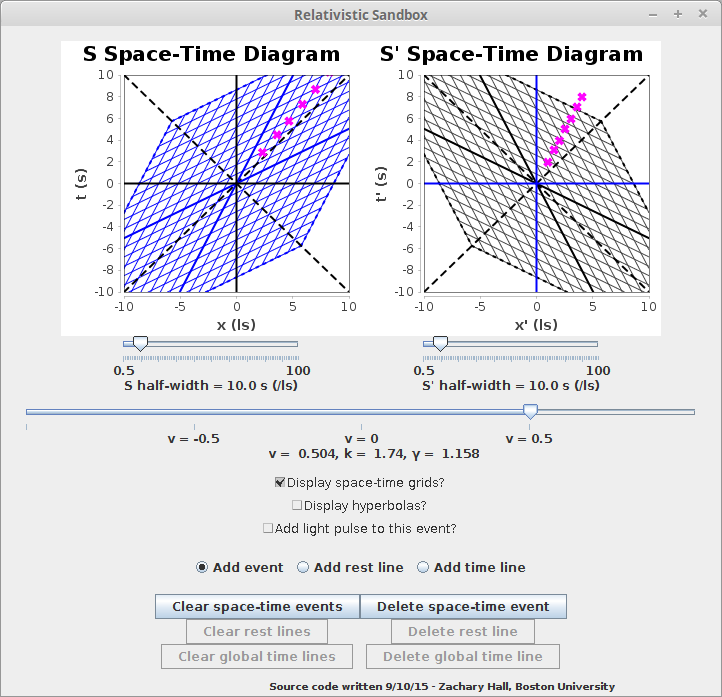
We can also see what this looks like over the hyperbolic structure of the spacetime:
We can see visually that, even though the velocity is not twice that of the original velocity (0.5 c does not go to c), because of the definition of hyperbolic angle as the bound hyperbolic area , it is plausible that the hyperbolic angle, i.e. bounded area, does increase by a factor of 2 -- that it does indeed do so was shown mathematically above. The relation \( v = c\tanh A \) maps the interval \( v \in [-c,c] \) to \( A \in [-\infty,\infty]\) and thus, as an object is being continually boosted, i.e. as A is constantly increasing, the velocity measured will always be less than c.
The chronogeometry of Minkowski spacetime is hyperbolic owing to the constancy of the speed of light and thus of the quantity \(t^2 - x^2 \) (or \( t^2 - (\frac{x}{c})^2 \) in conventional units) for all observers. The value \( t^2 - (\frac{x}{c})^2 \) of an event is also the square of the proper time of that event if it is inside either the past or future null cones of the event (t,x) = (0,0), as it is the magnitude squared of the purely temporal interval an observer travelling straight from one event to another would measure. If \( t^2 - (\frac{x}{c})^2 \) is less than 0, the event is outside of the light-cone of the event x = t = 0, and the quantity \( x^2 - c^2t^2 \) is the square of the proper distance of that event with respect to the event x = t = 0, as it is magnitude squared of the purely spatial interval that an observer determining it to happen at t = 0 would measure via radar. If \( t^2 - (\frac{x}{c})^2 = 0 \), then the event is along the future or past null cone of the event x = t = 0 -- any electromagnetic processes caused by the event t = x = 0 must be on the future null cone and any electromagnetic processes that could have directly affected the event x = t = 0 must have reached the event t = x = 0 along the past null cone. The expression \( t^2 - (\frac{x}{c})^2 \) defines the spacetime metric of special-relativistic 2-D space-time, and encodes the above-examined hyperbolic nature of the space-time and its invariant null cone structure.
This annotated image from Wikipedia shows the nature of a hyperbolic rotation of spacetime coordinates more explicitly:
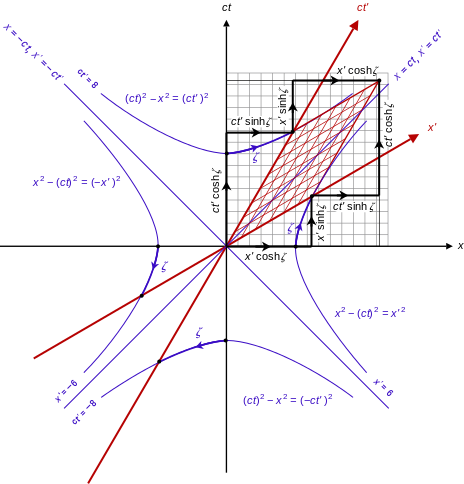
Let us now revisit the briefly discussed twin paradox. We saw, at the beginning of this lesson, that two observers moving relative to each other each said that events separated by some interval of time on each of each others' world-lines took a longer interval of time in each of their own frames. That is, the processes each underwent both appeared time dilated to each other. We saw that, in order for these world-lines to meet back up, one, or both, of these observers must accelerate. We showed, by considering that the temporal consequences of the acceleration of one of these observers can be described by that observer tossing their clock to a third observer moving with equal and opposite velocity relative to the first observer, that the observer undergoing accelerating would have aged less than the inertial observer upon returning to the same location.
Equipped with an understanding of hyperbolic chronogeometry, we are now in a position to understand more generally how initially coincident and synchronized clocks along various world-lines will compare if those world-lines intersect. Suppose, according to some observer who is not accelerating (this is easy for them to tell as it can be felt physically), some other observer moves along an arbitrary world-line which can in general accelerate. How do we relate the temporal intervals the arbitrarily accelerating observer undergoes to the temporal interval the inertial (constant velocity) observer undergoes? As we have seen, a non-accelerating, or inertial observer, is simply a system of space-time coordinates (t,x) for labelling events in the space-time. We have seen that, for another, relatively moving inertial observer, the value \( t^2 - (\frac{x}{c})^2 \) in this system of coordinates gives the square of the proper time of that relatively moving observer, i.e. the time as measured by the relatively moving observer it took the event (t,x) to occur. In the case of an arbitrarily relatively moving observer, we can consider, from event to event the arbitrarily moving relative observer undergoes, the infinitesimal quantity \( dt^2 - (\frac{dx}{c})^2 \) describing the separation of spatiotemporal separation of successive events comprising the relatively moving observer. Every infinitesimal interval \( dt^2 - (\frac{dx}{c})^2 \) as measured by the inertial observer will be a squared interval of the relatively moving observer's proper time. Thus, to find how much the relatively moving observer has aged throughout the world-line they took, we simply sum up all the \( \sqrt{dt^2 - (\frac{dx}{c})^2} \) according to the inertial observer:
where Δτ is the total proper time interval of the segment of the world-line considered and \( dτ = \sqrt{dt^2 - \Big(\frac{dx}{c}\Big)^2} \) is an infinitesimal proper time element.
Now,
$$ Δτ = \int\sqrt{1 - \Big(\frac{dx}{c dt}\Big)^2}dt = \int\sqrt{1 - \Big(\frac{v(t)}{c}\Big)^2}dt = \int\frac{dt}{γ(t)} \,, $$while the inertial observer of the coordinate system (t,x) ages
$$ Δt = \int dt \,, $$which is larger than the proper time.
Thus, in an inertial coordinate system, an observer undergoing relative motion to the observer at rest in that inertial coordinate system and returning to that observer will have aged less than the rest observer. In this sense, the straightest (i.e. inertial) path in a special-relativistic spacetime is the longest according to the spacetime metric of Special Relativity, and hence also proper time. This is the essence of the twin paradox.
Of course, our universe really has three spatial dimensions, not one as considered so far, and electromagnetic processes and entities with mass are in general free to move through any of them. The mathematical description of a special-relativistic spacetime with three spatial dimensions is called Minkowski spacetime. There are a number of more subtle phenomena with a full four dimensional Minkowski spacetime that are out of the scope of this lesson -- see, for example, Thomas precession, or the special-relativistic aberration of light. However, we can still draw a number of the same conclusions. It can easily be shown that, in the case of boosts along the so-called x direction, the y and z coordinates (coordinates along the spatial directions orthogonal to x) are unchanged between the relatively moving observers, i.e. y' = y and z' = z for all events in both space-time systems if the relative motion stays along x. But there is nothing special about the line in space we have called the x-axis -- it is just a name after all. Thus all of the same arguments introduced here would apply to relative motion along the so-called y and z directions: we are just renaming the spacetime! It follows that the invariant spacetime interval of a full four dimensional Minkowski spacetime in an inertial coordinate system is given by
$$ dτ^2 = dt^2 - \Big(\frac{dx}{c}\Big)^2 - \Big(\frac{dy}{c}\Big)^2 - \Big(\frac{dz}{c}\Big)^2 $$where the proper time of a four dimensional world-line is found by integrating the above expression as before. It is then easily shown by the same technique already applied to the case with one spatial dimension above that
$$ Δτ = \int\sqrt{1 - \Big(\frac{\vec{v}(t)⋅\vec{v}(t)}{c^2}\Big)}dt = \int\frac{dt}{γ(t)} $$where \( \vec{v}(t) = v_{x}(t)\hat{x} + v_{y}(t)\hat{y} + v_{z}(t)\hat{z} \) is the 3-velocity of the world-line as a function of time as determined by the inertial observer with the space-time coordinate system (t,x,y,z) and
$$ γ := \frac{1}{\sqrt{1 - \Big(\frac{\vec{v}⋅\vec{v}}{c^2}\Big)}} $$for three dimensions.
To download the applications, simply click on one of the three hyperlinks to the left of the page. This will download a .zip file for each
application. Then, unzip the .zip file. This will extract a folder of the same name as the .zip file (i.e. SANDBOX for SANDBOX.zip).
In this folder, there is a .jar file -- running this file launches the application. The file will not run if you remove it from the folder
it is in initially. The reason for packaging the application in this way is that the source code uses what is called an external library in Java.
A library is a set of objects (another piece of Java jargon) conveniently defined for a certain set of coding needs. The particular external library
used was JFreeChart , an open-source project, the creators of which I thank enormously.
Note that the .jar files are unsigned (but are safe to run)---look up how to open unsigned .jar files on your OS to run them. You may also need to update to the latest version of Java to
run the application properly.